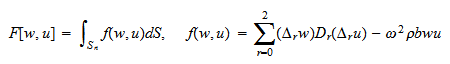 が常にゼロとなる
が常にゼロとなる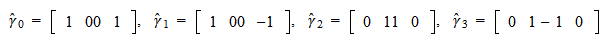 を用いて
を用いて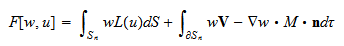 を得る.ここで,演算子
を得る.ここで,演算子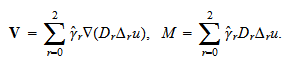 (eq.Fwithboundary)の右辺に存在する境界積分は,
境界
(eq.Fwithboundary)の右辺に存在する境界積分は,
境界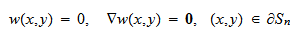 を境界条件としてテスト関数
を境界条件としてテスト関数細分化四角形要素を用いた
RTMによる散乱問題の数値解法
概要
逐次伝達法(RTM)は散乱問題に適した数値計算法であり, 散乱領域に発生する局在波を抽出できるという他にない特徴がある. このRTMは,弱形式離散化による空間メッシュを利用した定式化が提案されたことで 適用範囲が拡大した. しかし,これまでに弱形式離散化で利用されたメッシュ要素は長方形だけであった. 本研究の目的は,不等辺四角形を含むメッシュによりRTMを拡張できることを示すことである. なお,解析対象は4階の微分方程式で支配された弾性平板上の屈曲波である. 弱形式離散化においてメッシュ要素の不等辺四角形を細分化すると, 形状関数に力学的な条件を考慮したメカニカル形状関数を導入できる. しかも,このメカニカル形状関数の導入で, 多様な散乱領域の形状に対応できるばかりか, 解析精度の向上も可能になる .
逐次伝達法(RTM)は散乱問題に適した数値計算法であり, 散乱領域に発生する局在波を抽出できるという他にない特徴がある. この特徴を利用して電子波,マイクロ波,弾性波のシステムにおいて 散乱問題が議論されているAppelbaum,Hirose,weakFormDisc. RTMは弱形式離散化を用いた定式化により その適用範囲が拡大したweakFormDisc. 弱形式離散化は,空間をメッシュに分割することで 運動方程式を離散化する手法である. その際,入射波と反射波を進行方向によらず同等に離散化できると 計算精度を保つことができるので, 長方形のメッシュ要素が用いられていたKKI. しかし,長方形だけでは散乱領域のさまざまな形状に対応することが難しい. そこで, 弱形式離散化を不等辺四角形を含むメッシュに拡張することが本研究の目的である.
重調和解析の応用例として,また,実用的にも重要なことから, 屈曲波の散乱現象を検討対象として選んだ. 弱形式離散化の枠組みの中では, 屈曲変位を表す場の変数は空間座標に関する1階微分が メッシュ要素間で連続である必要があるZienkiewicz. その理由は, メッシュ要素間の力学的均衡条件から境界における1階微分の連続性を導出できないために, この条件がないと亀裂がない平板でも個々の要素が自由に回転するからである. 従って, 場の変数の関数値とその空間微分を離散化変数としてメッシュの各節点に割り当てるとともに, 形状関数を3次の多項式で構成した. 一般的には屈曲波が属する関数空間はSobolev空間であり, Argyris要素のように2階微分が可能な5次多項式で補間できることが知られているSolin. しかし,Argyris要素では辺上の自由度のために RTMで必要な擬似波面を定義できない. 本研究では補間多項式の次数を高くするよりも, 3次の補間多項式で構成できる形状関数を検討する.
シェル構造物の屈曲変形に有限要素解析を適用する際に, 四角形要素を三角形要素に細分化する試みが 行われているZienkiewicz,Brebbia. それらの試みは,形状関数の幾何学的な連続性を 限られた基底関数で実現するための基礎検討であった. これらの検討結果を利用できること,および,長方形へ連続的に変形が可能なことから, 不等辺四角形を含む弱形式離散化を提案する. その際,形状関数の役割として, 幾何学的な連続性だけを前提に関数を補間するにとどまらず, 力学的な制約条件を担うことが可能なことを示す. この新しい形状関数をメカニカル形状関数と名付けた. なお,弱形式離散化で利用する空間メッシュは有限要素法と同等であるが, 次の2つの事項が有限要素法とは異なっている: (i) メッシュの節点を仮想的な波面として利用する,および, (ii) 2階の差分方程式を導出することが目的である. なお,屈曲波は4階の微分方程式により支配されているが, 弱形式離散化は離散化変数をベクトルにすることで2階の差分方程式を導出できる. 弱形式離散化の拡張により, 散乱領域の多様な形状に柔軟に対応できるRTMの拡張も可能となる.
本論文の構成は次の通りである. 2節では,弱形式離散化を用いたRTMの定式化を擬似波面に言及しつつまとめる. 3節では,不等辺四角形を三角形要素で細分化するとともにメカニカル形状関数を提案する. さらに,空間メッシュがひずんだ場合に見かけ上生じる偽反射を評価し, RTMの解析精度を検討する. 4節はまとめである. また,付録Aには,空間微分を離散変数に含むことを前提として, 三角形要素の形状関数がまとめられている.
薄い弾性平板が![]() 平面にあるとする. この平板が角振動数
平面にあるとする. この平板が角振動数![]() で定常的に振動していると仮定し,
屈曲変形の横方向の変位すなわち散乱問題の場の変数を
で定常的に振動していると仮定し,
屈曲変形の横方向の変位すなわち散乱問題の場の変数を![]() で表す.
このとき,ある2次元領域
で表す.
このとき,ある2次元領域![]() において場の変数
において場の変数![]() を求めることは
任意のテスト関数
を求めることは
任意のテスト関数![]() に関して汎関数
に関して汎関数![]()
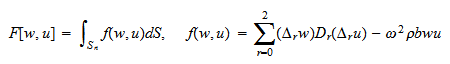 が常にゼロとなる
が常にゼロとなる![]() を求めること(ヌル値問題)と等価であるKKI,KKII. ここで,
を求めること(ヌル値問題)と等価であるKKI,KKII. ここで,![]() は面要素であり,
演算子
は面要素であり,
演算子![]() (
(![]() = 0, 1, 2)は,行列基底
= 0, 1, 2)は,行列基底 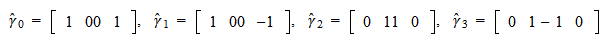 を用いて
を用いて![]() と定義されている. また,
と定義されている. また,![]() ,
,![]() ,
,![]() はそれぞれ弾性平板の剛性定数,質量密度,厚さである.
Gaussの定理を用いて(eq.F)を変形すると
はそれぞれ弾性平板の剛性定数,質量密度,厚さである.
Gaussの定理を用いて(eq.F)を変形すると 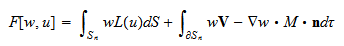 を得る.ここで,演算子
を得る.ここで,演算子![]() は
は ![]() と定義され,
と定義され,![]() は屈曲波の運動方程式である.
また,
は屈曲波の運動方程式である.
また,![]() と
と![]() は境界
は境界![]() に沿た曲線座標と法線ベクトル,
に沿た曲線座標と法線ベクトル,
![]() と
と![]() は境界での剪断力ベクトルとモーメントテンソルであり次の様に表現できる:
は境界での剪断力ベクトルとモーメントテンソルであり次の様に表現できる:
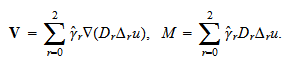 (eq.Fwithboundary)の右辺に存在する境界積分は,
境界
(eq.Fwithboundary)の右辺に存在する境界積分は,
境界![]() から剪断力とモーメントが平板に及ぼす力学的影響を表している.
さらに, 隣接した部分要素間の境界でこの積分項を一般的に考えると, 部分要素間の剪断力とモーメントの均衡衡関係を汎関数により考慮できる.
この均衡関係を利用して,隣接する部分要素間に成立する力学条件を, 2階の差分方程式として導出する方法が2.2節で論じる弱形式離散化である. このとき,
から剪断力とモーメントが平板に及ぼす力学的影響を表している.
さらに, 隣接した部分要素間の境界でこの積分項を一般的に考えると, 部分要素間の剪断力とモーメントの均衡衡関係を汎関数により考慮できる.
この均衡関係を利用して,隣接する部分要素間に成立する力学条件を, 2階の差分方程式として導出する方法が2.2節で論じる弱形式離散化である. このとき,
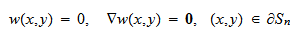 を境界条件としてテスト関数
を境界条件としてテスト関数![]() に課すと, (eq.Fwithboundary)で境界
に課すと, (eq.Fwithboundary)で境界![]() における積分項が失われ,
剪断力とモーメントの影響を見かけ上排除することもできる.
における積分項が失われ,
剪断力とモーメントの影響を見かけ上排除することもできる.
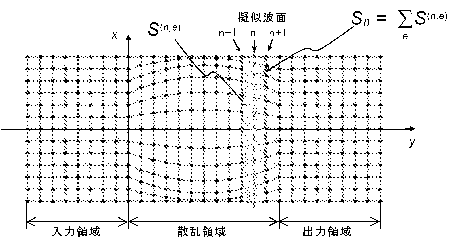
図1:弾性平板に よ る 導波路の 不等辺四角形を 含む メ接し て 不等辺四角形を 含む 部分要素S(n,e)が 存在.
図1に示したように, 導波路における2次元的な散乱問題を前提として,波の進行方向に![]() 軸を設ける.
入力波は,
軸を設ける.
入力波は,![]() から正の方向に入力すると仮定し,
空間を入力領域
から正の方向に入力すると仮定し,
空間を入力領域![]() ,散乱領域
,散乱領域![]() ,
出力領域
,
出力領域![]() の3つに分ける.
板の厚さや幅が空間的に変化すると入射波が散乱されるが, 離散化に際して空間メッシュにひずみがある場合にも見かけ上ではあるが反射が生じる.
図1では,空間が不等辺四角形を要素に含む四角形メッシュで分割されているが, この領域が見かけの散乱領域になる. さらに,
入力および出力領域が座標軸に平行な長方形要素により分割されている. 長方形要素を用いるとメッシュに局所的な空間反転と並進操作を行っても対称なことから,
離散化しても入射波と反射波を進行方向によらず同等に表現でき, 数値計算の精度を向上できる.
の3つに分ける.
板の厚さや幅が空間的に変化すると入射波が散乱されるが, 離散化に際して空間メッシュにひずみがある場合にも見かけ上ではあるが反射が生じる.
図1では,空間が不等辺四角形を要素に含む四角形メッシュで分割されているが, この領域が見かけの散乱領域になる. さらに,
入力および出力領域が座標軸に平行な長方形要素により分割されている. 長方形要素を用いるとメッシュに局所的な空間反転と並進操作を行っても対称なことから,
離散化しても入射波と反射波を進行方向によらず同等に表現でき, 数値計算の精度を向上できる.
メッシュの節点を2つの指標![]() と
と![]() を用いて 位置ベクトル
を用いて 位置ベクトル![]() で指定する.
このとき,波動が
で指定する.
このとき,波動が![]() 軸方向に進むと考え, 図に示したように,
指標
軸方向に進むと考え, 図に示したように,
指標![]() で指定できる疑似波面の存在を仮定する.
で指定できる疑似波面の存在を仮定する.
![]() 番目の疑似波面に接し
番目の疑似波面に接し![]() 番目の擬似波面に挟まれた
メッシュ要素を
番目の擬似波面に挟まれた
メッシュ要素を![]() (
(![]() = 1,2,3, ....,
= 1,2,3, ...., ![]() )と
指標
)と
指標![]() を用いて指定する(
を用いて指定する(![]() は要素の総数). 従来の弱形式離散化では,メッシュ要素
は要素の総数). 従来の弱形式離散化では,メッシュ要素![]() が長方形に限られていたがKKI, 不等辺四角形を含む場合を以下で議論する.
が長方形に限られていたがKKI, 不等辺四角形を含む場合を以下で議論する. ![]() および
および![]() 番目の擬似波面に挟まれた領域
番目の擬似波面に挟まれた領域![]() が, 弱形式離散化で使用される汎関数(eq.F)の積分領域
が, 弱形式離散化で使用される汎関数(eq.F)の積分領域![]() である.
である.
汎関数(eq.F)の積分領域![]() が, 四角形要素
が, 四角形要素![]() により構成されているとし,
その各頂点の位置座標を
により構成されているとし,
その各頂点の位置座標を![]() (
(![]() = 1,2,..,
= 1,2,..,![]() )
で表す.ここで,
)
で表す.ここで,![]() は四角形要素の頂点数である.
場の変数とその空間微分を要素とする3次元の縦ベクトル
は四角形要素の頂点数である.
場の変数とその空間微分を要素とする3次元の縦ベクトル![]() を
を
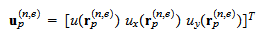 で定義し,以後,離散化変数と呼ぶ.ここで,
で定義し,以後,離散化変数と呼ぶ.ここで,![]() と
と![]() はそれぞれ
はそれぞれ![]() と
と![]() による
による![]() の偏微分を,
の偏微分を,![]() は転置を示す.さらに,
各頂点における離散化変数を成分とするベクトル
は転置を示す.さらに,
各頂点における離散化変数を成分とするベクトル![]() を
を ![]() で定義する. このとき,要素内部における
で定義する. このとき,要素内部における![]() を
を![]() を用いて補間できる(3節参照).
有限要素法で知られているように,節点での空間微分を考慮すると形状関数の補間精度を向上できる. しかし,屈曲波の解析では補間精度の向上もさることながら,
メッシュ要素ごとに平板の傾きが急変する現象を抑えるために必要であるSolin.
を用いて補間できる(3節参照).
有限要素法で知られているように,節点での空間微分を考慮すると形状関数の補間精度を向上できる. しかし,屈曲波の解析では補間精度の向上もさることながら,
メッシュ要素ごとに平板の傾きが急変する現象を抑えるために必要であるSolin.
テスト関数![]() も同様に
離散化変数
も同様に
離散化変数![]() から構成されたベクトル
から構成されたベクトル![]() を用いて場の変数と同じ形状関数により補間できる. 従って,ベクトル量
を用いて場の変数と同じ形状関数により補間できる. 従って,ベクトル量![]() ,
,
![]() を用いると, 補間表現により
を用いると, 補間表現により 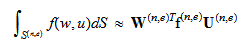 と積分を近似することができる.ここで,
と積分を近似することができる.ここで, ![]() は右辺が補間表現により得た近似であることを示す.
また,
は右辺が補間表現により得た近似であることを示す.
また,![]() は,形状関数に関する空間積分を成分とする
は,形状関数に関する空間積分を成分とする
![]() 行列である.
行列である.
![]() 番目の疑似波面上の節点
番目の疑似波面上の節点 ![]() (
(![]() = 0, 1, 2, ...,
= 0, 1, 2, ...,
![]() ) における離散化変数
) における離散化変数 ![]() をまとめ,疑似波面に割り当てられた
をまとめ,疑似波面に割り当てられた![]() 次元のベクトル
次元のベクトル ![]() を定義する. 同様にテスト関数
を定義する. 同様にテスト関数![]() を
を![]() 番目の擬似波面上で考え,
番目の擬似波面上で考え, ![]() 次元のベクトル
次元のベクトル![]() を定義できる.
このとき, 節点
を定義できる.
このとき, 節点![]() は,メッシュ要素
は,メッシュ要素![]() の頂点
の頂点
![]() (
(![]() = 1, 2, ...,
= 1, 2, ..., ![]() )の
いずれかと一致させる必要がある. このとき,行列
)の
いずれかと一致させる必要がある. このとき,行列![]() の各成分を並べ替えることで,
大域的な係数行列
の各成分を並べ替えることで,
大域的な係数行列![]() を構成し,汎関数(eq.F)を
を構成し,汎関数(eq.F)を 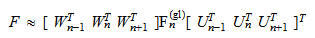 と表現できる.
ここで,テスト関数に関する境界条件(eq.BConw)を課すと,
と表現できる.
ここで,テスト関数に関する境界条件(eq.BConw)を課すと, ![]() と
と![]() はともに零ベクトルである.
このことにより,
はともに零ベクトルである.
このことにより, ![]() 番目と
番目と![]() 番目の擬似波面における
番目の擬似波面における![]() に関する境界条件を
見かけ上考慮しなくともよくなる. 係数行列
に関する境界条件を
見かけ上考慮しなくともよくなる. 係数行列![]() を
を
![]() で定義すると,
で定義すると,![]() が任意であることから
が任意であることから
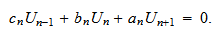 を導出することができる. この2階差分方程式は,
メッシュ要素が従う運動方程式とともに,
を導出することができる. この2階差分方程式は,
メッシュ要素が従う運動方程式とともに, ![]() 番目の擬似波面における剪断力およびモーメントの均衡を表現している.
一旦,2階の差分方程式が得られると,RTMの手順Appelbaum,Hirose
を変更することなく散乱問題を解析することができる.
番目の擬似波面における剪断力およびモーメントの均衡を表現している.
一旦,2階の差分方程式が得られると,RTMの手順Appelbaum,Hirose
を変更することなく散乱問題を解析することができる.
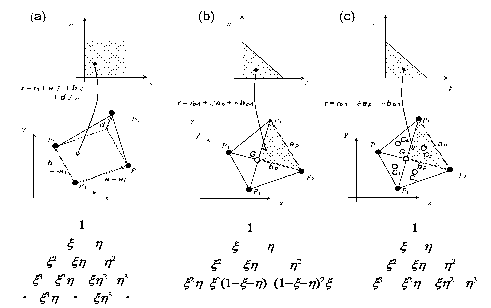
図2:局所的なξη空間か らxy空間中の 不等辺四角形要素へ の 写像,お よ び ,形状関数の 基底.基底の 個数は ,そ れ ぞ れ ,(a) 12, (b) 9, (c) 10.
図2(a)~(c)は,局所的な![]() 空間から
不等辺四角形が属する大域的な
空間から
不等辺四角形が属する大域的な![]() 空間への写像を模式的に示している.
この不等辺四角形は,図1に示した
空間への写像を模式的に示している.
この不等辺四角形は,図1に示した![]() であるが,
表記を簡潔にするために以後は指標(
であるが,
表記を簡潔にするために以後は指標(![]() )を省略する. 場の変数を補間する
)を省略する. 場の変数を補間する![]() と
と![]() の多項式
(即ち,形状関数)の基底をパスカルの三角形で示した. いずれも,弱形式離散化のメッシュ要素として使用できるが,
(a)と異なり(b)および(c)では不等辺四角形が三角形で細分されている. この細分化は,写像を線形化するとともに内部節点(白丸)での
自由度を利用してメカニカル形状関数を定義するために行った.
の多項式
(即ち,形状関数)の基底をパスカルの三角形で示した. いずれも,弱形式離散化のメッシュ要素として使用できるが,
(a)と異なり(b)および(c)では不等辺四角形が三角形で細分されている. この細分化は,写像を線形化するとともに内部節点(白丸)での
自由度を利用してメカニカル形状関数を定義するために行った.
不等辺四角形の頂点の位置ベクトル![]() (
(![]() = 1,2, .. ,
= 1,2, .. , ![]() )を用いると,
辺に沿ったベクトル
)を用いると,
辺に沿ったベクトル![]() を
を ![]() で定義できる(ただし,
で定義できる(ただし,![]() ).
このとき,図2(a)~(c)で示した局所空間から不等四角形への写像を 次のように表現できる. (a):
).
このとき,図2(a)~(c)で示した局所空間から不等四角形への写像を 次のように表現できる. (a): ![]() .
ただし,
.
ただし,![]() ,
, ![]() . (b)および(c):
. (b)および(c): ![]() . ただし,不等辺四角形の重心
. ただし,不等辺四角形の重心![]() の位置ベクトル
の位置ベクトル![]() を用いて,
を用いて, ![]() と定義.また,
と定義.また, ![]() ,
,
![]() .
(a)では写像が非線形であるが,(b)と(c)では線形化されている. 写像の線形・非線形の差異は,Jacobianの座標依存性の違いとしてのちに重要になる.
不等辺四角形の頂点
.
(a)では写像が非線形であるが,(b)と(c)では線形化されている. 写像の線形・非線形の差異は,Jacobianの座標依存性の違いとしてのちに重要になる.
不等辺四角形の頂点![]() と不等辺四角形の重心
と不等辺四角形の重心![]() に,
3次元ベクトルである離散化変数
に,
3次元ベクトルである離散化変数![]() と
と![]() を割り当てる(
を割り当てる(![]() = 1, 2, ...,
= 1, 2, ..., ![]() ). また,細分化三角形の重心
). また,細分化三角形の重心![]() には,
場の変数
には,
場の変数![]() のみを割り当てる(
のみを割り当てる(![]() ).
).
不等辺四角形の一辺![]() に属す2端点に,
関数値
に属す2端点に,
関数値![]() ,
, ![]() と 辺に沿った方向微分
と 辺に沿った方向微分 ![]() ,
,
![]() を割り当てることができる.
従って,辺に沿った
を割り当てることができる.
従って,辺に沿った![]() を補間するために使用する場の自由度は4であり,
3次の多項式で補間すると自由度の過不足がなく場の変数を一意に補間できる. しかも,辺を共有する隣接した要素なら, 要素ごとに独立に補間を行っても,
両者の補間値が辺の上で自動的に一致する. また,
を補間するために使用する場の自由度は4であり,
3次の多項式で補間すると自由度の過不足がなく場の変数を一意に補間できる. しかも,辺を共有する隣接した要素なら, 要素ごとに独立に補間を行っても,
両者の補間値が辺の上で自動的に一致する. また,![]() も辺の両端においてなら,
この両端を囲む要素間で一致する. 以上の理由から,補間多項式は3次式あることが好ましい.
も辺の両端においてなら,
この両端を囲む要素間で一致する. 以上の理由から,補間多項式は3次式あることが好ましい.
図2(a)の場合, 頂点に割り当てられた離散化変数の自由度が3![]() (=
12)であり. 基底もこれと同じ12個必要である. しかし,3次の多項式以下では基底の個数が10個までしか用意できない.
そこで,4次式である
(=
12)であり. 基底もこれと同じ12個必要である. しかし,3次の多項式以下では基底の個数が10個までしか用意できない.
そこで,4次式である![]() と
と![]() も基底として選んだ.
このとき,不等辺四角形の辺上では
も基底として選んだ.
このとき,不等辺四角形の辺上では![]() あるいは
あるいは![]() が0か1の定数なので,
少なくとも辺上では3次式の条件に一致する. しかし, Jacobian
が0か1の定数なので,
少なくとも辺上では3次式の条件に一致する. しかし, Jacobian ![]() が座標値に依存することから,
汎関数の積分の表現が複雑になり解析精度の低下をもたらす原因になった.
が座標値に依存することから,
汎関数の積分の表現が複雑になり解析精度の低下をもたらす原因になった.
Jacobianの座標値依存をなくすために, 辺![]() と不等辺四角形要素の重心
と不等辺四角形要素の重心
![]() で構成される4つの三角形
で構成される4つの三角形![]() を用いて不等辺四角形
を用いて不等辺四角形![]() を
細分化した. この場合も, Jacobianが細分化三角形ごとに変化するが,
座標変換の写像が線形であることより少なくとも三角形内部では定数である.
を
細分化した. この場合も, Jacobianが細分化三角形ごとに変化するが,
座標変換の写像が線形であることより少なくとも三角形内部では定数である.
図2(b)は細分化に三角形を用いた場合で, 細分化された三角形要素における離散化された場の自由度が9である.
この場合3次の基底全てを用いる必要はいが, 独立なものを選ぶ必要がありここでは ![]() ,
, ![]() ,
, ![]() とした. 一方,図2(c)は, 三角形の内部点
とした. 一方,図2(c)は, 三角形の内部点![]() (
(![]() )に場の変数の値のみを
離散化の自由度として追加した場合で,自由度の総数は10である. この場合,有限要素法で使用されるHermite要素Solinを利用でき,
3次までの単項式の全てを基底として使用した.
)に場の変数の値のみを
離散化の自由度として追加した場合で,自由度の総数は10である. この場合,有限要素法で使用されるHermite要素Solinを利用でき,
3次までの単項式の全てを基底として使用した.
図2に示した3つの方式のメッシュ要素をRTMで使用するためには, 2.2.1で論じた擬似波面を設定できる必要がある. (a)の場合,不等辺四角形の頂点を結ぶことで従来と同様に擬似波面を設定できる. しかし,(b)と(c)の方式では,白丸で示した内部節点が存在するために 空間反転対称性と並進対称性を満たす擬似波面を設定できなかった. この問題を解決するために, 内部節点に割り当てた離散化の自由度を, 不等辺四角形の頂点に割り当てた自由度と関連付けることにした. この関連付けを用いて内部自由度を見かけ上取り除いた形状関数が, 次節に示すメカニカル形状関数である.
図2(b)に示した細分化した不等辺四角形要素![]() の各頂点
の各頂点![]() (
(![]() = 1, 2, ...,
= 1, 2, ..., ![]() )と内部節点
)と内部節点![]() に,離散化変数
に,離散化変数![]() と
と![]() が割り当てられている.
さらに,細分化三角形
が割り当てられている.
さらに,細分化三角形![]() に, 3
に, 3![]() (=
9)次元の縦ベクトル
(=
9)次元の縦ベクトル ![]() を割り当てることができる. この離散化変数を用いると,
付録Aに示した手順により, 場の変数
を割り当てることができる. この離散化変数を用いると,
付録Aに示した手順により, 場の変数![]() を補間することができる.
同様に,テスト関数
を補間することができる.
同様に,テスト関数![]() についても3
についても3![]() 次元のベクトル
次元のベクトル![]() を用いて補間できるので,
汎関数(eq.F)の積分領域を細分化三角形
を用いて補間できるので,
汎関数(eq.F)の積分領域を細分化三角形![]() で置き換えて次式を導出できる:
で置き換えて次式を導出できる:
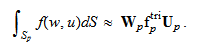 ここで,
ここで,![]() は
は![]() の行列である.
の行列である.
![]() の成分である
の成分である![]() (
(![]() = 1,2, ...,
= 1,2, ..., ![]() )と
)と![]() を再配置して,
内部頂点での成分
を再配置して,
内部頂点での成分![]() とそれ以外の成分
とそれ以外の成分
![]() =
=
![]() に分けて,
に分けて, ![]() と分離して表現する.
また,テスト関数の離散化変数
と分離して表現する.
また,テスト関数の離散化変数![]() の成分も同様に再配置して
の成分も同様に再配置して
![]() と表すと, 不等辺四角形
と表すと, 不等辺四角形![]() に関する汎関数を, (eq.FSp)の
に関する汎関数を, (eq.FSp)の![]() に関する和を用いて
に関する和を用いて
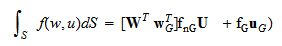 と表すことができる. ここで,
と表すことができる. ここで, ![]() と
と![]() はそれぞれ, 行列
はそれぞれ, 行列![]() の成分を組み替えて再構成した
の成分を組み替えて再構成した
![]() および
および ![]() の行列である.
の行列である.
汎関数を(eq.Fwithboundary)のように境界積分を含む形で表現すると,
細分化三角形あるいは不等辺四角形内における場の変数が 境界における剪断力とモーメントの影響下にあることが分かる. しかし, 境界![]() でテスト関数とその勾配がゼロであると見なして
でテスト関数とその勾配がゼロであると見なして![]() を課すと,
この境界での積分項を取り除くことができ, 剪断力とモーメントが境界で任意の値を取る場合を考慮できる. このとき,汎関数(eq.intSne)のヌル値問題から,
内部節点に割り当てられた自由度と同じ本数の連立1次方程式を導出でき,
を課すと,
この境界での積分項を取り除くことができ, 剪断力とモーメントが境界で任意の値を取る場合を考慮できる. このとき,汎関数(eq.intSne)のヌル値問題から,
内部節点に割り当てられた自由度と同じ本数の連立1次方程式を導出でき, 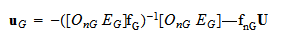 を得る. ここで,
を得る. ここで,![]() は
は![]() の零行列,
の零行列,![]() は
は![]() の単位行列である. 従って,
の単位行列である. 従って,
![]() と定義し,さらに,
と定義し,さらに,![]() の零行列
の零行列![]() を用いて
を用いて ![]() を
を
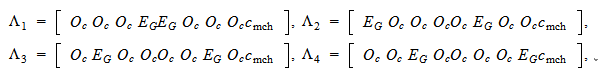 で定義すると,付録Aで定義されている三角形要素の形状関数
で定義すると,付録Aで定義されている三角形要素の形状関数![]() を用いて
を用いて
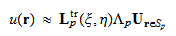 と補間できる. ここで,記号
と補間できる. ここで,記号![]() は,
細分化三角形
は,
細分化三角形![]() を点
を点![]() を含むように選ぶことを意味している.
補間関数
を含むように選ぶことを意味している.
補間関数 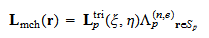 は,平板の力学的な条件を考慮した不等辺四角形の形状関数である.
従って,(eq.mechShape)の各成分をメカニカル形状関数と名付ける.
図2(c)のように細分化三角形が内部節点
は,平板の力学的な条件を考慮した不等辺四角形の形状関数である.
従って,(eq.mechShape)の各成分をメカニカル形状関数と名付ける.
図2(c)のように細分化三角形が内部節点![]() (
(![]() = 1, 2, ...,
= 1, 2, ..., ![]() )を含む場合は, 上述の議論に,この点における場の変数の値
)を含む場合は, 上述の議論に,この点における場の変数の値![]() を追加して
を追加して ![]() を
を![]() などと変更することで同じ議論ができる.
などと変更することで同じ議論ができる.
形状関数を定義する際に内部節点の自由度を見かけ上排除する手法が 文献Brebbia,Zienkiewiczでも議論されている. しかし,それらは場の変数が幾何学的な接続を保つことを条件としている. 本方式の独自性は, 弱形式理論を利用して力学的な役割を形状関数に付加したことにある. さらに, 必要に応じてエネルギーフラックスの保存則など別の力学的な条件を付加することも可能であり, さまざまな法則を担保させ得る拡張性がある.
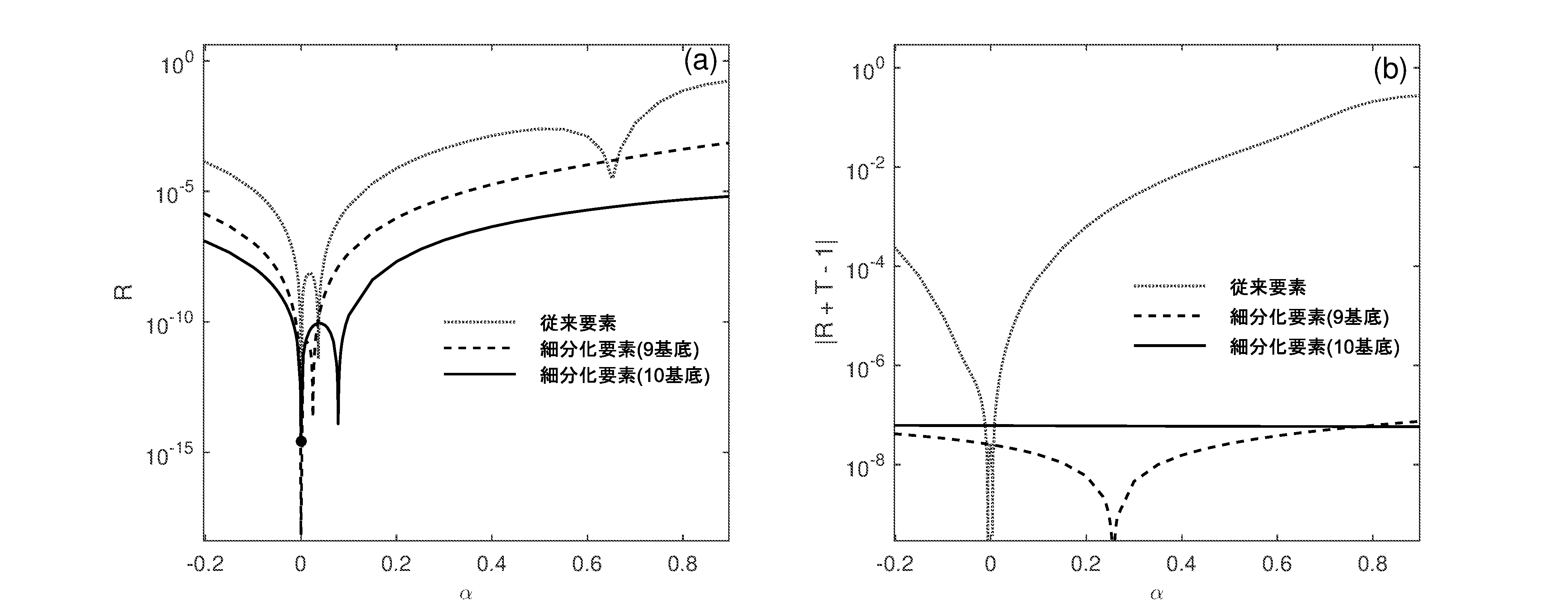
図3.ひ ず み パ ラメータαに よ る 偽反射の
変化.(a)偽反射率R,(b)エネルギ ー保存側か ら の 乱れ\R + T - 1\.
厚さの一様な平板で作られた導波路を定常的に進む屈曲波は一切反射しないが, 離散化に際してひずんだメッシュを用いると見かけの反射が生じる.
従って, 意図的にメッシュをひずませて発生するこの偽反射を調べることで, 数値計算の精度を評価することができる.
また,反射率と透過率をそれぞれ![]() と
と![]() で表すと, エネルギー保存から
で表すと, エネルギー保存から![]() が成立するはずである.
従って,
が成立するはずである.
従って,![]() はエネルギー保存側の乱れを定量的に表現している.
そこで,
はエネルギー保存側の乱れを定量的に表現している.
そこで,![]() とメッシュひずみの関係を調べることで,
数値計算の精度を評価することができる.
とメッシュひずみの関係を調べることで,
数値計算の精度を評価することができる.
図3にRTMにより求めた (a)見かけ上発生する偽反射率![]() と(b)エネルギー保存側の乱れ
と(b)エネルギー保存側の乱れ![]() が示されている.
RTMによる計算手順の詳細は文献KKIと同じである.
横軸はひずみパラメータ
が示されている.
RTMによる計算手順の詳細は文献KKIと同じである.
横軸はひずみパラメータ![]() で,長方形格子のメッシュをひずませる効果を持つ.
計算する領域の
で,長方形格子のメッシュをひずませる効果を持つ.
計算する領域の![]() 軸および
軸および![]() 軸の下限値をそれぞれ
軸の下限値をそれぞれ
![]() および
および![]() として, ひずみのない長方形メッシュの節点を,
として, ひずみのない長方形メッシュの節点を, ![]() (
(![]() = 0, 1, 2, ...,
= 0, 1, 2, ..., ![]() ,
, ![]() = 0, 1, 2, ...,
= 0, 1, 2, ..., ![]() ) で定義する. このとき,
) で定義する. このとき,![]() の範囲で節点を
の範囲で節点を
![]() とひずませた. 従って,
とひずませた. 従って,
![]() でひずみのない長方形メッシュが,
でひずみのない長方形メッシュが,
![]() で長方形の一部が完全につぶれたメッシュが得られる.
図1(a)に示したひずんだメッシュは,
で長方形の一部が完全につぶれたメッシュが得られる.
図1(a)に示したひずんだメッシュは,![]() = 0.9のときの様子である. 計算に用いた緒元は,アルミニュウムが材料であると考え次の値を用いた: 入射波の周波数
= 0.9のときの様子である. 計算に用いた緒元は,アルミニュウムが材料であると考え次の値を用いた: 入射波の周波数![]() = 15kHz, 散乱領域の幅
= 15kHz, 散乱領域の幅![]() = 13mm, 空間の分割幅
= 13mm, 空間の分割幅![]() = 1.3333mm,
= 1.3333mm, ![]() = 1.0833mm. 弾性平板の幅
= 1.0833mm. 弾性平板の幅![]() = 16mm, 厚さ
= 16mm, 厚さ![]() = 1mm, Young率
= 1mm, Young率![]() = 71GPa, Poison比
= 71GPa, Poison比![]() = 0.32, 質量密度
= 0.32, 質量密度![]() kg/m.
剛性定数は
kg/m.
剛性定数は![]() ,
, ![]() で得られる.
で得られる.
図3において,点線で示した曲線が従来の不等辺形四角形を要素として用いた結果で, 図2(a)の場合に対応する.
また,破線と実線で示された曲線が細分化四角形要素を用いた場合で, それぞれ 図2の(b)および (c)に対応している. 図3
(a)では,いずれの曲線も![]() = 0で小さな値を取り, 例外があるものの
= 0で小さな値を取り, 例外があるものの![]() の絶対値が増加するにつれて増加する傾向がある.
点線と比較したその他曲線の相対的値は,
の絶対値が増加するにつれて増加する傾向がある.
点線と比較したその他曲線の相対的値は, ![]() が大きくなると破線で2桁,実線で4桁程度改善されている.
これらの改善は,メカニカル形状関数を用いたことにある.
が大きくなると破線で2桁,実線で4桁程度改善されている.
これらの改善は,メカニカル形状関数を用いたことにある.
図3 (b)はエネルギー保存則の乱れ![]() を示している.
この図でも,ひずみパラメータ
を示している.
この図でも,ひずみパラメータ![]() がゼロから離れるに従い,
点線と比較して破線と実線の値が相対的に抑制される傾向があり, その抑制量は最大3桁を超えている. なお,
がゼロから離れるに従い,
点線と比較して破線と実線の値が相対的に抑制される傾向があり, その抑制量は最大3桁を超えている. なお,![]() = 0.28付近で破線の値が著しく低下しているが, それは
= 0.28付近で破線の値が著しく低下しているが, それは![]() の符号が偶然に反転することが原因である.
の符号が偶然に反転することが原因である.
これまで,RTMで使用できる弱形式離散化のメッシュ要素は長方形に限られていた. その理由は,RTMの定式化に必要な擬似波面を定義できること,および, 離散化した進行波の特徴が進行方向により変わらないことにあった. 本研究は,入力および出力領域に設けた長方形要素に連続的な変形で接続できる不等辺四角形を 用いてRTMを再定式化した. このとき,不等辺四角形を三角形要素に細分化すると, 次のような利点があることを示した: (i) 従来方法と同様に擬似波面を定義できる. (ii) 散乱領域の多様な形状に柔軟に対応できる. (iii) 従来方法と比較して,偽反射およびエネルギー保存則の乱れを 低減した高い精度の解析ができる. これらの利点は, メカニカル形状関数の導入により実現できた. メカニカル形状関数はRTMに適用できるばかりではなく, メッシュ分割を行うどのような数値解析にも適用できる手法である.
\appendix
不等辺四形要素![]() が図2(b)に示した細分化三角形
が図2(b)に示した細分化三角形![]() に分割されており,
その頂点が位置ベクトル
に分割されており,
その頂点が位置ベクトル![]() (
(![]() = 1, 2, ...,
= 1, 2, ..., ![]() (=4))で与えられているとする.
また,内部節点を
(=4))で与えられているとする.
また,内部節点を![]() で表す.
このとき,場の変数の離散化変数(eq.uu)を用いて,
で表す.
このとき,場の変数の離散化変数(eq.uu)を用いて, ![]() 内における場の変数を補間する関数,
即ち, 形状関数の表現をまとめる. なお,本節では簡潔にするために指標
内における場の変数を補間する関数,
即ち, 形状関数の表現をまとめる. なお,本節では簡潔にするために指標![]() を省略する.
を省略する.
要素![]() の辺に沿った線形独立なベクトルが
の辺に沿った線形独立なベクトルが
![]() で定義できる.
このとき,細分化要素
で定義できる.
このとき,細分化要素![]() 内の位置ベクトル
内の位置ベクトル![]() は,
局所空間の座標
は,
局所空間の座標![]() ,
, ![]() を用いて
を用いて
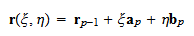 と表される. ただし,
と表される. ただし, ![]() ,
, ![]() を満たす. 局所座標
を満たす. 局所座標![]() から大域的な座標
から大域的な座標![]() へ変換する写像のJacobianは
へ変換する写像のJacobianは
![]() で与えられる定数であり,面積要素は
で与えられる定数であり,面積要素は
![]() と変換される. さらに,変数
と変換される. さらに,変数![]() ,
, ![]() の勾配は
の勾配は
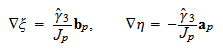 で与えられ,三角形要素ごとに異なるものの同じ三角形要素中では変化しない.
で与えられ,三角形要素ごとに異なるものの同じ三角形要素中では変化しない.
細分化三角形での補間に必要な基底の数は, 図2(b)でパスカルの三角形により示した9つである. これらをまとめた横ベクトル![]() を
を ![]() で定義する. さらに,
で定義する. さらに, ![]() の行列
の行列![]() を
を ![]() で定義し,
で定義し, ![]() =
= ![]() を用いて,形状関数を
を用いて,形状関数を![]() で定義する. また, 離散化変数
で定義する. また, 離散化変数
![]() を要素とする9次元のベクトル
を要素とする9次元のベクトル
![]() =
=
![]() を定義する. ここで,
を定義する. ここで,![]() は[
は[![]() ]
= 1+mod(
]
= 1+mod(![]() ,4)を示す. このとき,場の変数を
,4)を示す. このとき,場の変数を 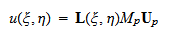 と補間できる. ここで,
と補間できる. ここで,![]() は
は![]() と
と![]() に関する方向微分を,
に関する方向微分を,
![]() と
と![]() に関する方向微分に変換する行列であり,
に関する方向微分に変換する行列であり,
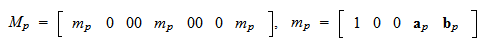 と定義されている. 従って,
と定義されている. 従って, ![]() に関する補間式は,点
に関する補間式は,点![]() がどの細分化三角形
がどの細分化三角形![]() に属するかで変化し,
に属するかで変化し,
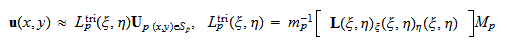 と表される. ここで,行列
と表される. ここで,行列![]() の第1行を
の第1行を
![]() と表せば,これは
9次元の横ベクトルでありその各成分が形状関数である. なお,類似した形状関数がHermite要素で使用されいるSolin. この形状関数は,本節で論じた補間方法との比較すると,
細分化三角形内に内部節点を設定し10個の基底を用いている. Hermite要素は図2(c)の場合に利用されている.
と表せば,これは
9次元の横ベクトルでありその各成分が形状関数である. なお,類似した形状関数がHermite要素で使用されいるSolin. この形状関数は,本節で論じた補間方法との比較すると,
細分化三角形内に内部節点を設定し10個の基底を用いている. Hermite要素は図2(c)の場合に利用されている.
J. A. Appelbaum and D. R. Hamann, ``Self-consistent electronic structure of solid surfaces", Physical Review B, 6 (1972), 2166--2177.
K. Hirose and M. Tsukada, ``First-principles calculation of the electronic structure for a dielectrode junction system under strong field and current", Physical Review B, 51 (1995), 5278--5290.
H. Kato and H. Kato, ``New formulation for the recursive transfer method using the weak form thery framework and its application to microwave scattering", IEICE Transactions: Fundamentals, E96-A (2013), 2698--2708.
H. Kato and H. Kato, ``An application of recursive transfer method to flexural waves I: A discretisation scheme using weak form theory and waveguide modes on inhomogeneous static plates", IEICE Transactions: Fundamentals, E97-A (2014), 1075--1085.
O. C. Zienkiewicz and R. L. Taylor, The finite element method, volume2: Solid and fluid mechanics dynamics and non-linearity (Forth ed.), McGrawHill, London, 1989.
P. Solín, Partial differential equations and the finite element method, John Wiley & Sons, Hoboken, 2006.
C. A. Brebbia and J. J. Connor, Fundamentals of Finite Element Techniques for Structural Engineers, Butterworths, London, 1973.
H. Kato and H. Kato, ``An application of recursive transfer method to flexural waves II: Reflection enhancement caused by resonant scattering in acoustic waveguide", IEICE Transactions: Fundamentals, E98-A (2014), 354--361.